Výpočetní geometrie
Vyučující
Rozsah výuky
2 + 2
Semestr
Z
Kredity
6
Zakončení
Z + Zk
Rozvrh
B4M39VG
Anotace
Cílem výpočetní geometrie je analýza a návrh efektivních algoritmů pro určování vlastností a vztahů geometrických objektů. Řeší se problémy geometrického vyhledávání, problém polohy bodu, hledání konvexní obálky množiny bodů v d‑rozměrném prostoru, problém hledání blízkých bodů, výpočet průniků polygonálních oblastí a poloprostorů, geometrie rovnoběžníků. Seznámíme se s novými směry návrhu algoritmů. Výpočetní geometrie nachází uplatnění nejen v geometrických aplikacích, ale i v obecných vyhledávacích problémech.
Přednášky
1.Výpočetní geometrie (VG), typické aplikace, techniky návrhu efektivních algoritmů
2.Geometrické vyhledávání - lokalizace oblasti pro zadaný bod
3.Geometrické vyhledávání - range search
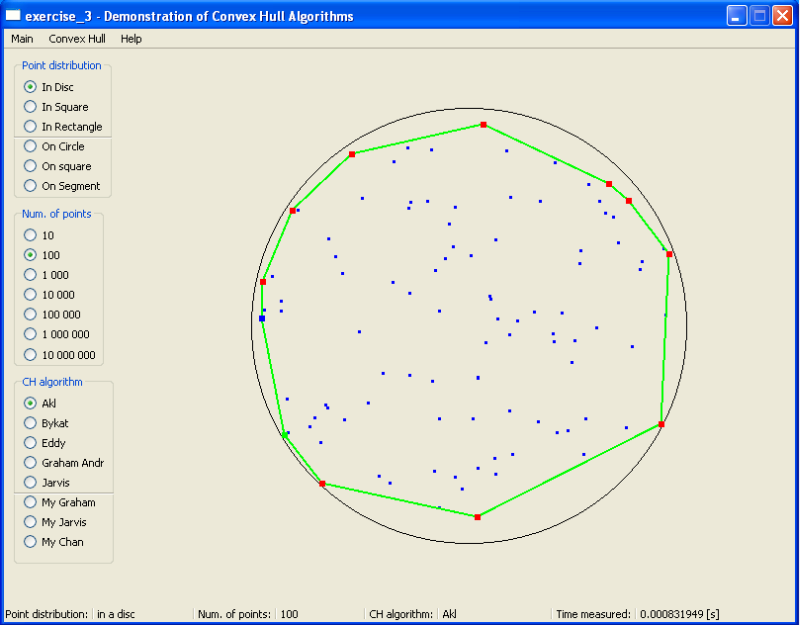
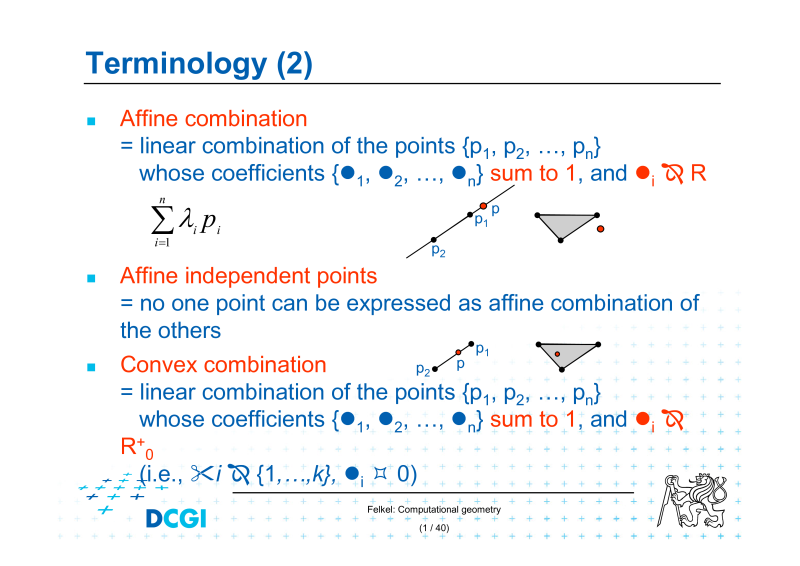
4.Konvexní obálka množiny bodů v rovině
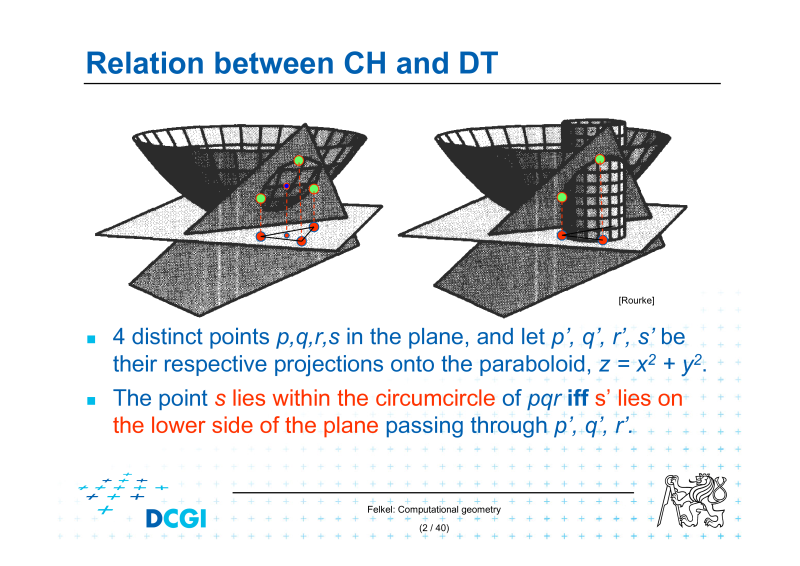
5.Konvexní obálka množiny bodů v prostoru
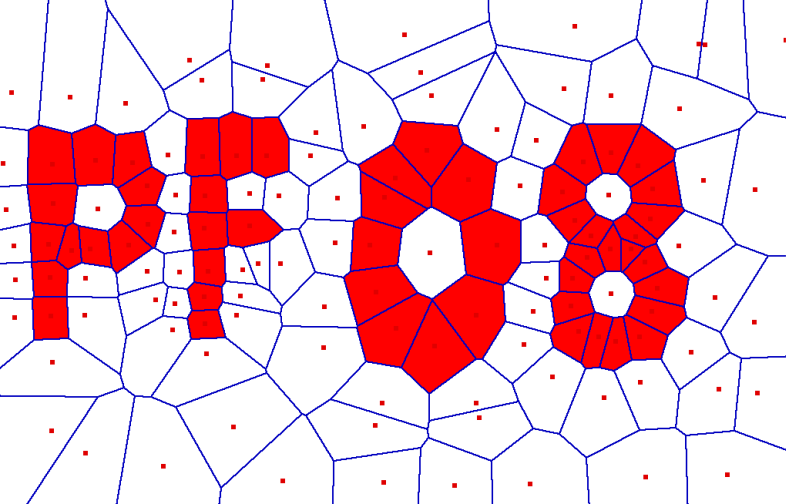
6.Voronoiův diagram množiny bodů
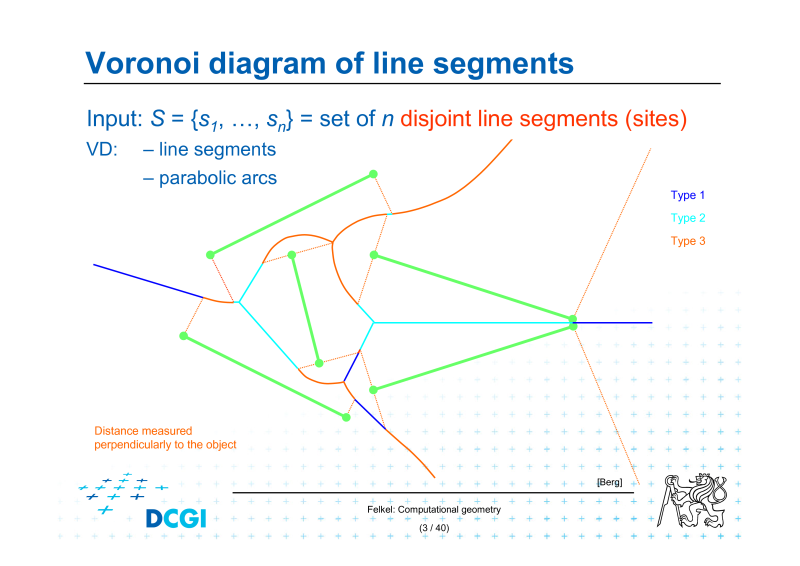
7.Voronoiův diagram úseček, Voronoiovy diagramy vyšších řádů
8.Planární triangulace
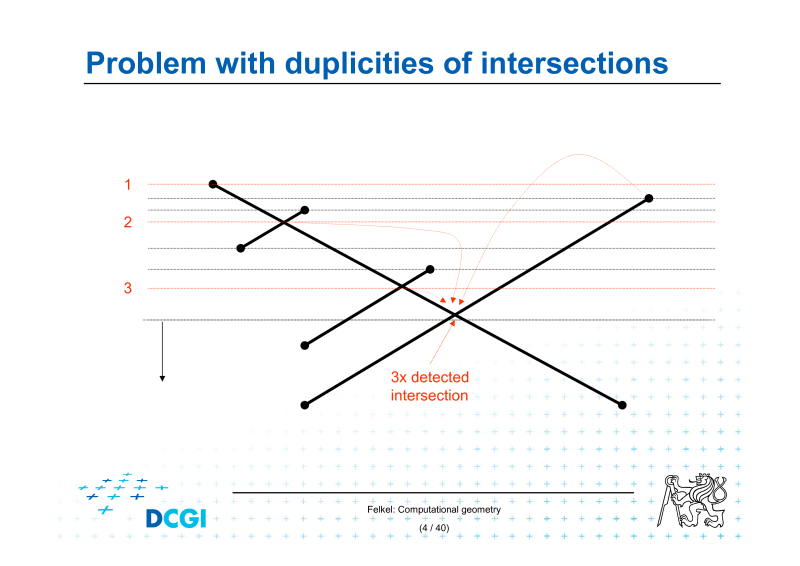
9.Algoritmy výpočtu průsečíků množiny úseček.
10.Průsečík množiny úseček s obdélníkovým oknem
11.Arrangementy
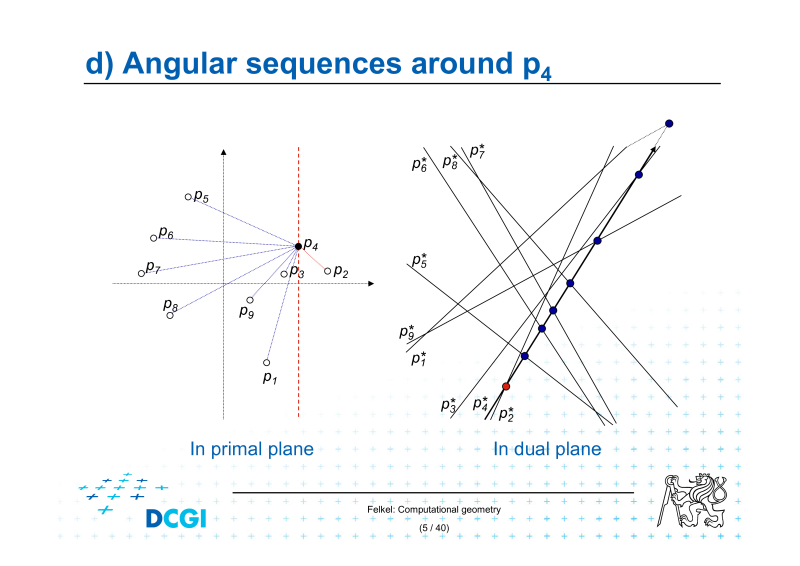
12.Duální algoritmy.
13.Nové směry v návrhu algoritmů
Cvičení
1.Seznámení s formou cvičení. Výběr témat. Robustnost geometrických predikátů
2.Samostatná příprava prvních vystoupení
3.Vystoupení na zadané téma, diskuse. Hodnocení materiálů a projevu ostatními studenty, náměty na vylepšení.
4.Vystoupení na zadané téma
5.Vystoupení na zadané téma
6.Vystoupení na zadané téma
7.Vystoupení na zadané téma
8.Vystoupení na zadané téma
9.Vystoupení na zadané téma
10.Vystoupení na zadané téma
11.Vystoupení na zadané téma
12.Vystoupení na zadané téma
13.Zápočet
14.Rezerva
Literatura a zdroje
- Berg, M. de, Cheong, O., Kreveld, M. van, Overmars, M.: Coputational Geometry. Algorithms and Applications, Springer-Verlag, Berlin, 3rd ed., 2008.
- Rourke, Joseph: Computational Geometry in C, Cambridge University Press, 2.vydání, 2000.
- Preperata F.P.- M.I.Shamos: Computational Geometry An Introduction. Berlin, Springer-Verlag, 1985.