Optimizing portfolio heuristics for optimal planning

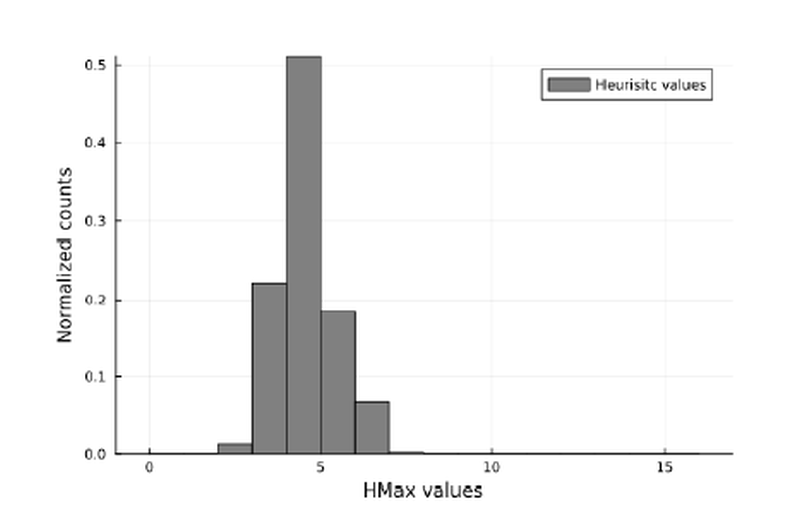
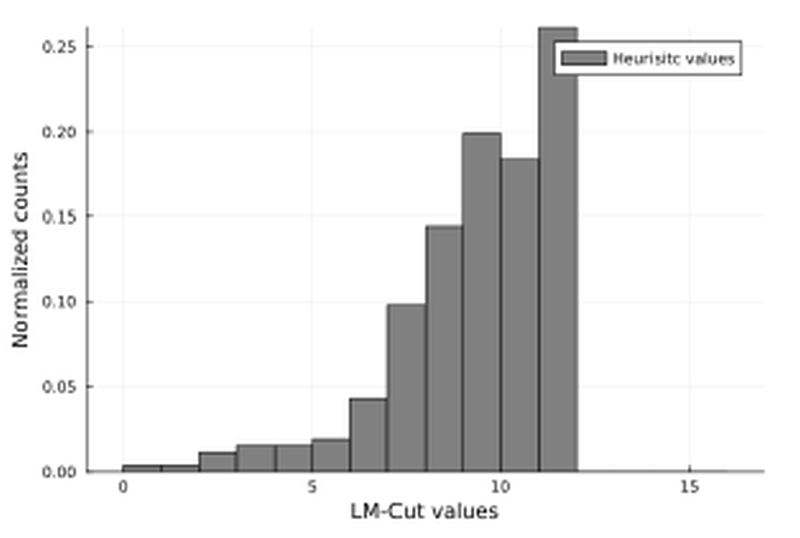
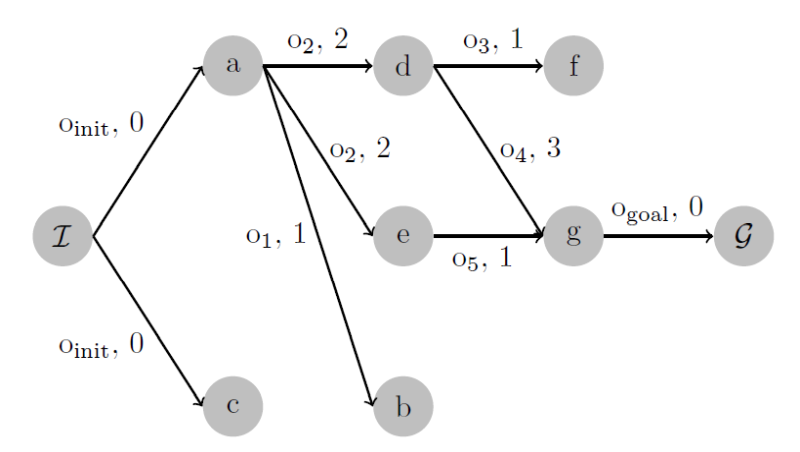
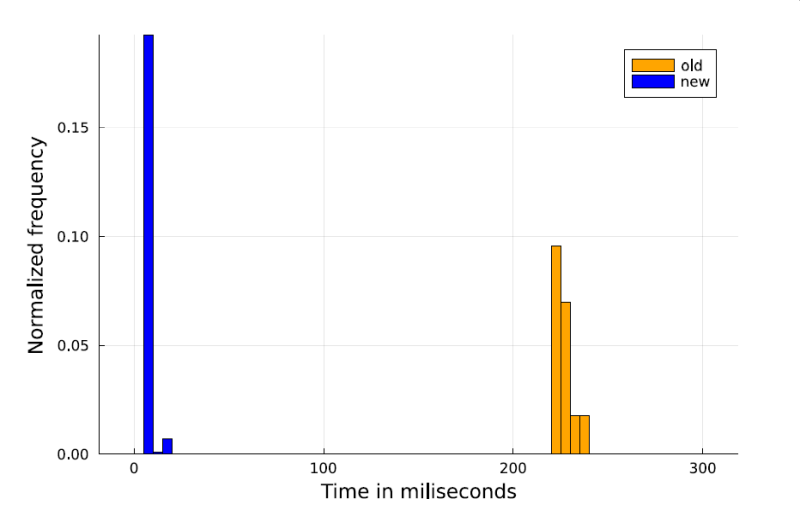
Finding an optimal plan (solution) to a planning problem can be a task unsolvable in a reasonable time. So it is important to efficiently comb the state-space of the problem. One viable option is the A* planner the efficiency of which is heavily reliant on the heuristic function used, it should both give good information and be admissible. This work is focused on the finding of these heuristics. This is achieved by training a neural network to output a series of numbers to be used as convex weights for already existing admissible planning heuristics. The heuristic created as a convex combination of admissible heuristics is also an admissible heuristic, and when used with the A* planner an optimal solution is guaranteed to be found. The heuristic is focused on lowering the number of expanded states by the A* planner, and therefore lowering the overall time of plan finding. This work discusses the advantages and disadvantages of this approach as well as the fundamental limit on performance.