Fast Approximation to Spherical Harmonic Rotation

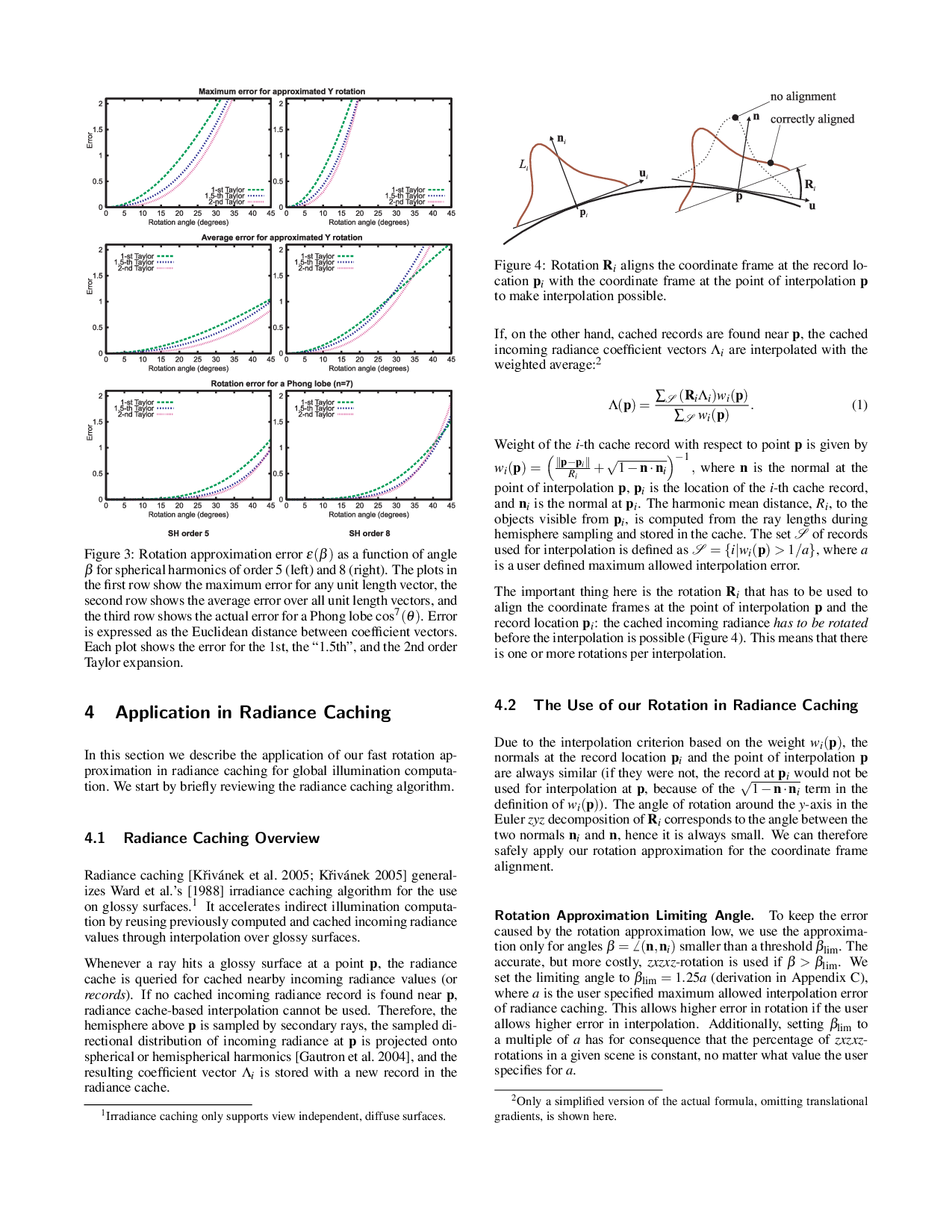
Rotation of functions represented by spherical harmonics is an important part of many real-time lighting and global illumination algorithms. For some of them a per-vertex or even per-pixel rotation is required, which implies the necessity of an efficient rotation procedure. The speed of any of the existing rotation procedures is, however, not able to meet the requirements of real-time lighting or fast global illumination. We present an efficient approximation of the spherical harmonic rotation applicable for small rotation angles. We replace the general spherical harmonic rotation matrix by its truncated Taylor expansion, which significantly decreases the computation involved in the rotation. Our approximation decreases the asymptotic complexity of the rotation---the higher the order of spherical harmonics, the higher the speed-up. We show applications of the proposed rotation approximation in global illumination and real-time shading. Although the rotation approximation is accurate only for small rotation angles, we show this is not a serious limitation in our applications.