Cache-efficient Graph Cuts on Structured Grids

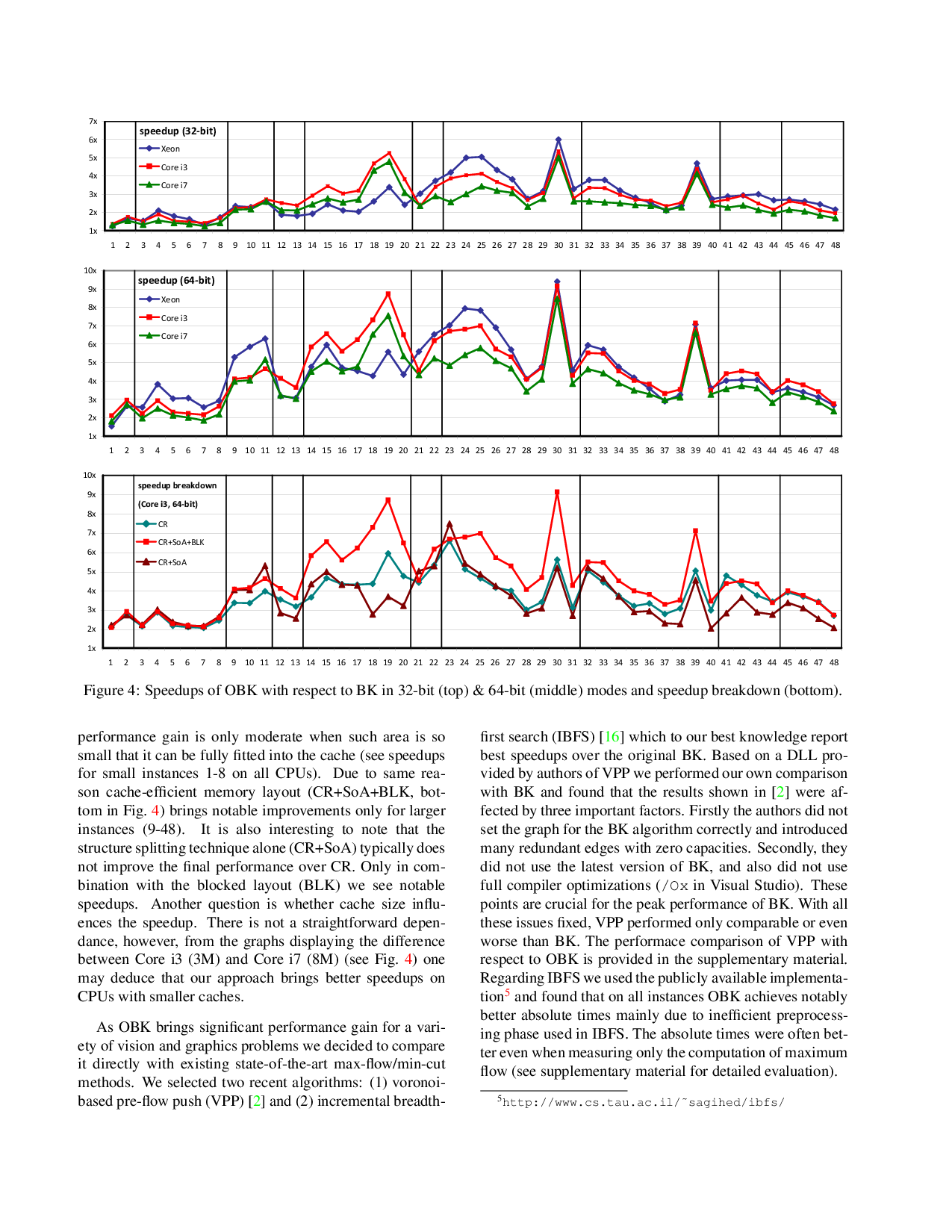
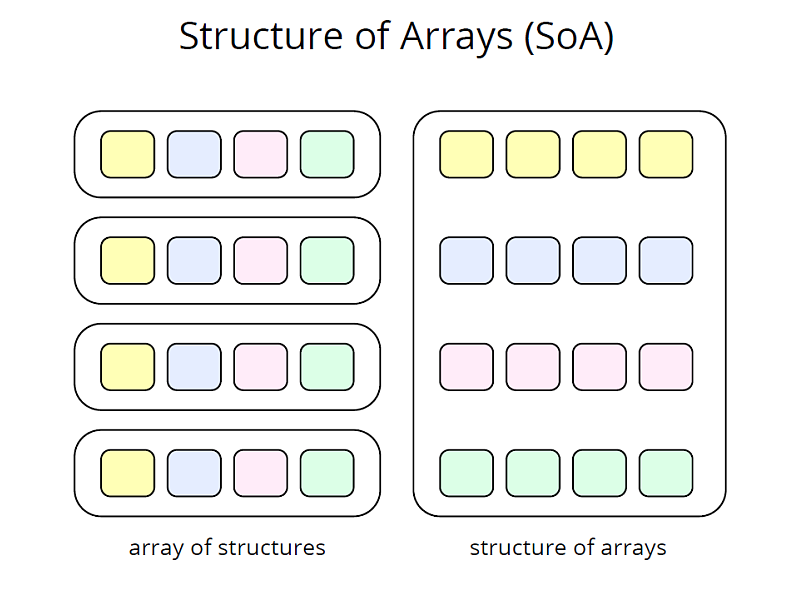
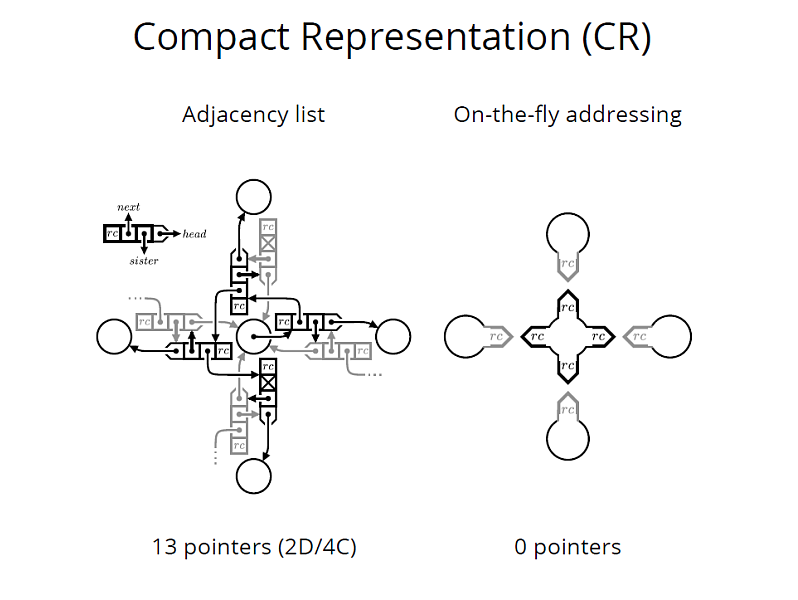
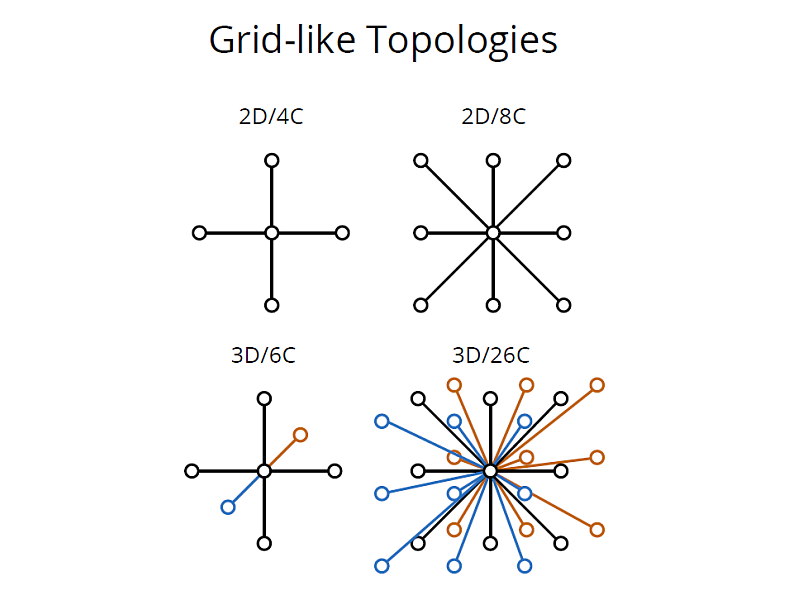
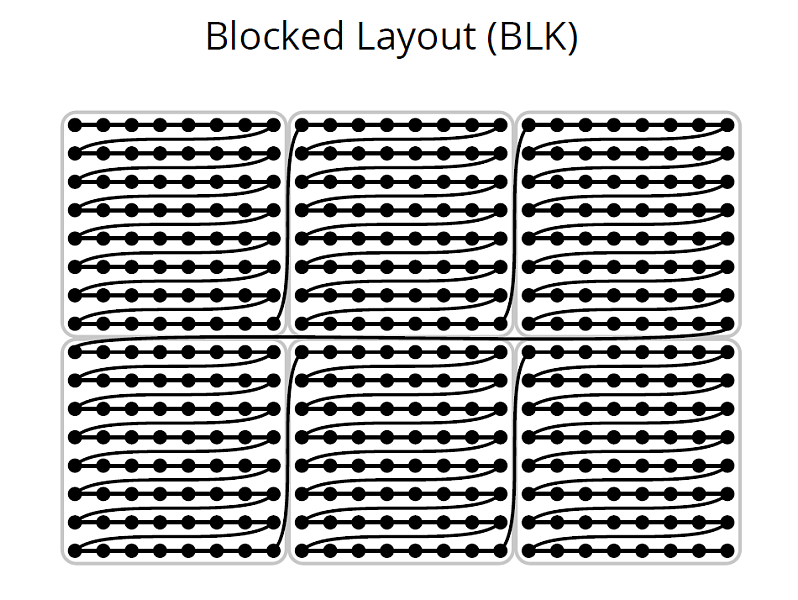
Finding minimal cuts on graphs with a grid-like structure has become a core task for solving many computer vision and graphics related problems. However, computation speed and memory consumption oftentimes limit the effective use in applications requiring high resolution grids or interactive response. In particular, memory bandwidth represents one of the major bottlenecks even in today's most efficient implementations. We propose a compact data structure with cache-efficient memory layout for the representation of graph instances that are based on regular N-D grids with topologically identical neighborhood systems. For this common class of graphs our data structure allows for 3 to 12 times higher grid resolutions and a 3- to 9-fold speedup compared to existing approaches. Our design is agnostic to the underlying algorithm, and hence orthogonal to other optimizations such as parallel and hierarchical processing. We evaluate the performance gain on a variety of typical problems including 2D/3D segmentation, colorization, and stereo. All experiments show an unconditional improvement in terms of speed and memory consumption, with graceful performance degradation for graphs with increasing topological irregularities.